1.-La bicicleta de Fer tiene ruedas con un diámetro de 50 cm. Fer quiere visitar a Ceci que vive a 2 km de su casa y quiere saber cuántas vvueltas dará su bicicleta para llegar a la casa de Ceci, ¿Cómo puede calcularlo?
P=π x d
P= 3.1416 x 50cm= 157.07 cm
2000000/157.07=1273.31
Vueltas: 1273.21
2.-Alfredo desea saber cuál es la ecuación de la trayectoria de un caballo que se encuentra amarrado a una estaca por una cuerda de 2 m cuando la cuerda está completamente tensa y suponiendo que el origen se encuentra en la estaca. Muéstrale a Alfredo el procedimiento para calcular lo anterior.
x2+y2=22
x2+y2=22
3.- Una circunferencia con centro en el origen y el radio r se puede expresar matemáticamente por:
x2+y2=22
x2+y2=42
x2+y2=72
x2+y2=1.52
x2+y2=9.52
4.-Calcula el radio de las siguientes circunferencias:
x2+y2=16
x2+y2=16
x2+y2=42
x2=9-y2
x2+y2=9
x2+y2=32
x2+y2=12
x2+y2=12
x2+y2=3.462
x2+y2=1/4
x2+y2=.25
x2+y2=.52
x2+y2=4/9
x2+y2=44
x2+y2=.812
5.-El radar de un avión registra la trayectoria de un ciclón. Si el centro del ciclón esta en C (0,0) y cada anillo concéntrico de la imagen del radar tiene 1 unidad de ancho, determina la ecuación de la tercera circunferencia que encierra la mayor parte del ciclón.
x2+y2=32
6.- Alejandra lanza una piedra a un lago, las ondas que se originan tienen forma circular. Si el punto donde cayó la piedra es el origen de un sistema de coordenada y la onda se aleja 3 unidades en cada segundo, ¿Cuál es la ecuación de la onda después de 3 segundos?
x2+y2=92
7.- Axel es campesino, para regar su siembra usa un aspersor que lanza el roció en forma circular alcanzando hasta un diámetro de 8 unidades. Si el aspersor se encuentra en el origen de un sistema de coordenadas, halla la ecuación de la circunferencia que describe el roció de riego.
x2+y2=82
8.- Alberto se subió en la feria a un juego mecánico que se asemeja al siguiente:
La rueda mayor tiene 4 m de radio. Las ruedas menores tienen 2m de diámetro.
Si coloca el origen del sistema de referencia en el centro de la rueda más grande, el quiere saber.
¿Cuál es la ecuación de cada una de las ruedas menores en la posición mostrada?
Azul
C (0,4)
(x-h)2+(y-k)2=r2
(x-0)2+(y-4)2=12
(x-0)2+(y-4)2=1
x2+y2-8y+16=1
x2+y2-8y+16-1=0
x2+y2-8y+15=0
A=π x r2
P= π x d
A=3.14
P= 6.28
Amarilla
(x-h)2+(y-k)2=r2
(x-4)2+(y-0)2=12
(x-4)2+(y-0)2=1
x2-8x+16+y2=1
x2+y2-8y+16-1=0
x2+y2-8x+15=0
A=π x r2
P= π x d
A=3.14
P= 6.28
Verde
(x-h)2+(y-k)2=r2
(x-0)2+(y+4)2=12
(x-0)2(y+4)2=1
x2+y2+8y+16=1
x2+y2+8y+16-1=0
x2+y2++8y+15=0
A=π x r2
P= π x d
A=3.14
P= 6.28
Naranja
(x-h)2+(y-k)2=r2
(x+4)2+(y-0)2=12
(x+4)2+(y-0)2=1
x2+8x+16+y2=1
x2+y2+8x+16-1=0
x2+y2+8x+15=0
A=π x r2
P= π x d
A=3.14
P= 6.28
9.-Determina la ecuación de la circunferencia y su grafica en su forma ordinaria para los centros y radios dados:
C(4,2) r=3
(x-h)2+(y-k)2=r2
(x-4)2+(y-2)2=32
(x-4)2+(y-2)2=9
C(-6,8) r=1/2
(x-h)2+(y-k)2=r2
(x+6)2+(y-8)2=.502
(x+6)2+(y-8)2=.25
C(3,-3) r=.6
(x-h)2+(y-k)2=r2
(x-3)2+(y+3)2=.62
(x-3)2+(y+3)2=.36
C(-4,-5) r=.77
(x-h)2+(y-k)2=r2
(x+4)2+(y+5)2=.772
(x+4)2+(y+5)2=.592
C(-6,9) r=1.41
(x-h)2+(y-k)2=r2
(x+6)2+(y-9)2=1.412
(x+6)2+(y-9)2=1.98
10.- Determina las coordenadas del centro y el radio de cada una de las circunferencias siguientes.
(x- ¾)2 + (y-3)2=81/4
(x-h)2+(y-k)2=r2
(x+3/4)2+(y+3)2=4.5
C (.75,3) = 4.5
(x-0.4)2+(y-2.4)2=37
(x-h)2+(y-k)2=r2
(x+.4)2+(y+2.4)2=6.08
C (.4,2.4) = 6.08
(x-2/5)2 + (y- ½)2 = ¼
(x-h)2+(y-k)2=r2
(x+2/5)2+(y+.5)2=.5
C (.4,.5) = .5
(x+3)2+y2-36=0
(x-h)2+(y-k)2=r2
(x-3)2+(y+36)2=0
C (-3, 36) =
x2+(y-1)2=6
(x-h)2+(y-k)2=r2
(x)2+(y+1)2=6
C (0,1) = 6
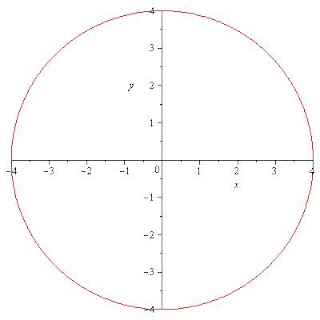
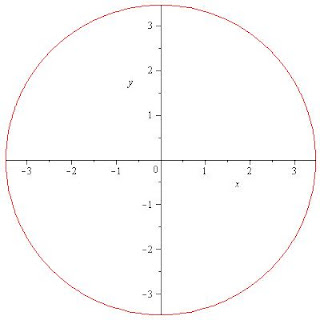
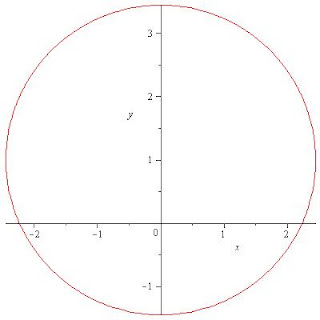
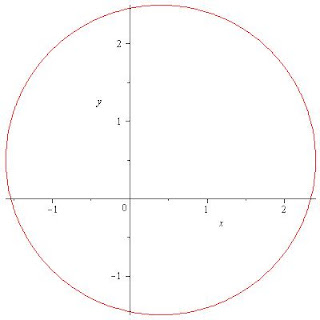
11.-Realiza la grafica de las siguientes circunferencias:
(x-2)2+(y-3)2=49
(x-2/5)2+(y-1/2)2=4
(x-5)5+(y-9)2=20
(x-6)2+y2-81=0
x2+(y+5)2=25
(x-1/2)2+(y+1/4)2=9
12.-Dadas las siguientes graficas encuentran la ecuación:
(x-h)2+(y-k)2=r2
C(-3,-3) r=5
(x+3)2+(y-3)2=52
(x+3)2+(y-3)2=25
(x-h)2+(y-k)2=r2
C(5,4) r=4
(x-5)2+(y-4)2=42
(x-5)2+(y-4)2=16
(x-h)2+(y-k)2=r2
C(-5,-5) r=2
(x+5)2+(y+5)2=22
(x+5)2+(y+5)2=4
(x-h)2+(y-k)2=r2
C(-2,0) r=7
(x+2)2+(y-0)2=72
(x+2)2+(y-0)2=49
(x-h)2+(y-k)2=r2
C(8,-8) r=1.2
(x-8)2+(y+8)2=1.22
(x-8)2+(-y+8)2=1.44
(x-h)2+(y-k)2=r2
C(-3,-3) r=6
(x+3)2+(y+3)2=62
(x+3)2+(y+3)2=36
13.-La ecuación de la circunferencia es (x-5)2+(y-3)2=39 muestra que el punto (5,-2) esta dentro de la circunferencia y que el punto (-1,5) esta afuera.
(x-5)2+(y-3)2=39
(x-h)2+(y-k)2=r2
C(5,3) r=6.2
14.-Determina la ecuación de la circunferencia cuyo centro es C (6, -2) y que es tangente al eje Y.
(x-h)2+(y-k)2=r2
(x-6)2+(y+2)2=62
(x-6)2+(y+2)2=36
15.- Determina la ecuación de la circunferencia cuyo centro es C (-3,5) y que es tangente a la recta x=7.
(x-h)2+(y-k)2=r2
(x+3)2+(y-5)2=112
(x+3)2+(y-5)2=121
16.- Determina la ecuación de la circunferencia que pasa por el punto (7,-5) y es tangente a la recta 2x-2y-8=0 en el punto (3,-1)
(x-h)2+(y-k)2=r2
(x-7)2+(y+5)2=72
(x-7)2+(y+5)2=49
17.-La ecuación de la circunferencia es (x+2)2+(y-3)2=36 determina la ecuación de la tangente a la circunferencia que pasa por el punto (3,3).
18.-Halla la ecuación de la circunferencia de radio 7 cuyo centro esta en la intersección de las rectas 3x-2y-24=0 y 2x+7y+9=0
19.- Halla la ecuación de la circunferencia que tiene diámetro con extremos en (3,6) y (-8,6).
C(-2.5 , 6) r=5.5
(x-h)2+(y-k)2=r2
(x+2.5)2+(y-6)2=5.52
(x+2.5)2+(y-6)2=30.25
20.-El rector de Laguna Verde se compone de dos cilindros concéntricos separados por una distancia de 3 unidades. En un simulador se hace un corte trasversal y se traza un sistema de coordenadas donde el circulo exterior de ubica en el tercer cuadrante y es tangente a los ejes X y Y. Si el radio del circulo interior es de 2.5 unidades, determina la ecuación de cada recta.
No hay comentarios:
Publicar un comentario